1592. Bridge
n people come to a river in the night. There is a narrow bridge, but it
can hold only two people at a time. They have one torch and, because it's
night, the torch has to be used when crossing the bridge. The movement across
the bridge without a torch is prohibited.
Each person has a different
crossing speed; the speed of a group is determined by the speed of the slower
member. Your job is to determine a strategy that gets all n
people across
the bridge in the minimum time.
Input. Consists of multiple test cases. The first line of
each test case contains the number of people n (n ≤ 103), and the second line gives
the sequence of n numbers – the crossing
times for each of the people. Nobody takes more than 104
seconds to
cross the bridge.
Output. For each test case print the
next information. The first line must contain the total number of seconds
required for all n people to cross
the bridge. The following lines give a strategy for achieving this time. Each
line contains either one or two integers, indicating which person or people
form the next group to cross. Each person is indicated by the crossing time
specified in the input. Although many people may have the same crossing time
the ambiguity is of no consequence. Note that the crossings alternate
directions, as it is necessary to return the flashlight so that more may cross.
If more than one strategy yields the minimal time, any one will do.
|
Sample input |
Sample output |
|
4 1 2 5
10 3 1 2 3 |
17 1 2 1 5 10 2 1 2 6 1 2 1 1 3 |
SOLUTION
greedy
Algorithm analysis
Sort the
time it takes people to cross the river in ascending order. Let ti be the time of
crossing the river by the i - th
person (t1 £ t2 £ … £ tn).
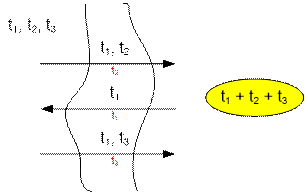
Consider how one, two, or three people should cross the bridge. For n = 1 and n = 2, the
optimal speed of crossing the river, respectively, is t1 and t2 = max(t1, t2) (the speed of
movement of two people is equal to the speed of the slow one). In the case of three people (n = 3), the first and second go to the other
side, the fastest (first) comes back with a lantern and transfers the third.
Thus, the optimal time to
cross the river is t1 + t2 + t3.
Consider the case when n
> 3. Let A £ B £ … £ Y £ Z be the people sorted by time of crossing
the bridge in increasing order (A is the fastest, Z is the slowest). Let J be
the person with whom Z moves. If J stays on the other side and never returns
back over the bridge, then it is optimal to choose it equal to Y. If J returns,
then it is optimal to choose it as the fastest, that is, A. Thus Z can cross the
bridge either with Y or A.

Compute the passage times of the
two slowest people (Y and Z) according to these two strategies.
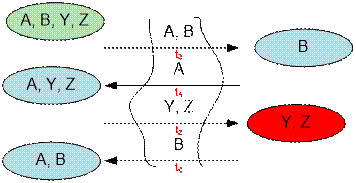
1. Z goes with Y. But then
before that there must be somebody who will return the lantern, for example K. This K also had
to be taken to the other side in order to return the lantern, and give it to Y and
Z. Let it be L.
Thus, K and L must return. To minimize the time, the two fastest should be
selected as K and L, that is, A and B. The passage time for Y and Z is tA + 2tB + tZ.
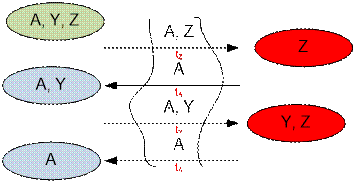
2. Z crosses the bridge together with A, then A returns. Then A crosses the bridge with Y and A returns. To go to another side of the river for Y
and Z takes 2tA + tY + tZ time.
In both cases,
only two slowest people cross the
bridge. The strategy (first or second) is chosen depending which of the values
(tA + 2tB + tZ or 2tA + tY + tZ) is less. If initially n people should cross
the bridge, then n – 2 people must do it recursively.
Example
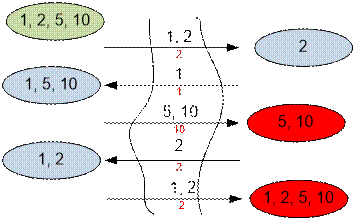
Sort the times of crossing the
bridge: 1, 2, 5, 10. Here tA = 1, tB = 2, tY = 5, tZ = 10. The passage time of the two
slowest people according to the first and second strategies are respectively
equal
·
tA + 2tB + tZ = 1 + 2
* 2 + 10 = 15;
·
2tA + tY + tZ = 2 * 1
+ 5 + 10 = 17;
Since the first
value is less, then Z should go with Y. Z with Y cross the bridge in time 15, after which it remains to go for A and B to the
other bank. This is done in time max{tA, tB} = 2.
The total time
to cross the bridge is 15 + 2 = 17.
Algorithm realization
Array m stores
the time of people to cross the river.
int m[1001];
Function go(n, visible)
returns the optimal time in which n people
can cross the river. The variable visible = 1, if the moving strategy itself
should be printed, and visible = 0 otherwise.
int go(int n,int visible)
{
int First, Second, Best;
One person crosses the river.
if (n == 1)
{
if (visible) printf("%d\n",m[0]);
return m[0];
} else
Two people cross the river.
if (n == 2)
{
if (visible) printf("%d %d\n",m[0],m[1]);
return m[1];
} else
Three people cross the river.
if (n == 3)
{
if (visible)
{
printf("%d %d\n",m[0],m[1]);
printf("%d\n",m[0]);
printf("%d %d\n",m[0],m[2]);
}
return m[0]
+ m[1] + m[2];
};
Compute the optimal
time First and Second for
the first and the second strategies described above.
First = m[0] + 2 * m[1] + m[n-1];
Second = 2 * m[0] + m[n-2] + m[n-1];
Best = (First < Second) ? First : Second;
if (visible)
{
if (Best == First)
{
printf("%d %d\n",m[0],m[1]);
printf("%d\n",m[0]);
printf("%d %d\n",m[n-2],m[n-1]);
printf("%d\n",m[1]);
} else
{
printf("%d %d\n",m[0],m[n-2]);
printf("%d\n",m[0]);
printf("%d %d\n",m[0],m[n-1]);
printf("%d\n",m[0]);
}
}
Recursively
compute the optimal strategy for the remaining n – 2 people.
return Best + go(n-2,visible);
}
The main part of
the program. Read the
number of test cases, read the time it
takes for people to cross the bridge into array m.
while(scanf("%d",&n)
== 1)
{
for(i = 0; i < n; i++) scanf("%d",&m[i]);
Sort the times
of crossing the river in ascending order.
sort(m,m+n);
Run function go
with parameter visible = 0, that returns the
optimal river crossing time. Print it, and then run function go again with parameter visible = 1, that prints the sequence of movements.
res = go(n,0);
printf("%d\n",res);
res = go(n,1);
}